les figures simples du plan... :
Sur une feuille de papier, un tableau nous avons un morceau d'un plan, c'est à dire une surface "plane " comme la surface de l'eau "tranquille" dans une bassine, un récipient quelconque, un étang , un lac. Un plan est infini, la surface du tableau , d'une feuille de papier , de l'écran d'ordinateur sont un tout petit morceau de plan. sur le plan on peut y dessiner :
- un point , que l'on représente souvent par un petit disque plein ou
non , ou le croisement de 2 segments ETC, bien qu'un point n'ait ni
volume, surface ou dimension quelconque. Dans la figure ci dessous
quelques représentions d'un point isolé, ou non. Le croisement de
lignes courbes on non , définissent un point au croisement de celle
ci.
- une droite, de longueur infini
- une demi droite, qui a une seule extrémité et se prolonge à l'infini
- un segment de droite, un morceau , un fragment de droite
limité par 2 points qui en sont les extrémités
- une ligne coube ou brisée, fermée ou non
- une ligne courbe
- des figures plus complexes ....
retour menu
Angles
Deux demi-droites qui ont même extrémités forment un angle, les deux
demi-droites en sont les côtés, l'extrémité commune en est le sommet.
On qualifie ces angles en fonction de leur "ouverture" comme
vous le
verrez
avec ce fichier ggb ici. Bougez le curseur pour faire varier
l'angle alpha, une demi droite reste fixe, la seconde qui a même
extrémité que la première , le sommet O de l'angle, va pivoter autour de
0. Vous découvrirez les différents noms des angles, les angles saillants
et leurs appellation, les angles rentrants selon leur "ouverture".
Angles opposés la figure
tirées du site Géogébra montre ce que sont des
angles opposés par le sommet et leurs propriétés, selon la
position du curseur: complètement à gauche ou à droite.
Droites, demi-droites, remarquables
Bissectrice d'un angle
Comment construire une bissectrice , la demi-droite qui
divise un angle en deux angles, adjacents, égaux. On trouve dans le site Géogebra la description de cette construction, sauf qu'elle fait apparaître deux points supplémentaires, le risque étant qu'en construisant à la règle et au compas l'apprenant, maladroit, inattentif ou peu appliqué trace une droite qui ne passera pas par le sommet sans qu'il en soit gêné. La construction d'un seul point suffit puisque la bissectrice passe par le sommet déjà existant, comme le montre une variante qui détaille le processus de construction, pour dérouler la construction utiliser le curseur à droite du titre; peu à peu apparaissent les étapes expliquées de la construction, en faisant varier les rayons des cercles de construction on découvre la façon de faire le bon choix
pour un résultat optimal.
Médiatrice d'un segment:
Construction. On observe souvent que l'apprenant, pour construire la médiatrice d'un segment, prend pour seul écartement du compas la longueur du segment , il construit plus ou moins pécisément les 2 sommets de 2 triangles équilatéraux, sans savoir qu'il s'agit de ceux-ci. les trois fichiers proposés tendent à s'adapter à la figure telle qu'elle est, sur le papier, et à rechercher une construction précise en construisant 2 points de la médiatrice, aussi éloignés l'un de l'autre, donc équidistants des extrémités du segment:
- on dipose de place de part et d'autre du segment , on choisit un écartement unique pas forcément égal à la longueur du segment. DEUX fichiers sont proposés voir ce cas "facile". Pour éviter un dessin trop chargé le premier fichier décrit la méthode et permet de visualiser le choix optimum du rayon du cercle. Le second fichier permet de faire défiler pas à pas la construction, il suffit de déplacer le curseur noir.
- Le segment, mal placé sur la feuille ne permet pas d’utiliser la méthode simple présentée par les fichiers cités plus haut, un troisième fichier aborde ce cas
Droites parallèles
Ce fichier montre
la construction à la règle et au compas d'une droite parallèle à une
autre et passant par un Point B . Ici construction, passant par B, de la
droite parallèle à la droite AA1. Pour suivre la démarche placer de
curseur t sur 0, puis déplacer jusque 6, le descriptif du processus
apparaît et le paragraphe est précédé du nombre suivi de/. La
construction repose sur les propriétés d'une sécante à deux droites
parallèles et l'égalité des angles alterne interne et de sa réciproque.
retour menu
Triangles
Le fichier extrait de Wikipedia donne un bon aperçu du vocabulaire et des éléments associés au triangle. Du plus quelconque au plus remarquable, visualisez les triangles et leur qualification en fonction de leur spécificité.A côté du triangle quelconque, on trouve des triangles qui se distinguent par des propriétés spécifiques:
- triangle isocèle
- triangle équilatéral
- triangle rectangle qui peut
être, aussi isocèle.
la longueur d'un côté est toujours inférieur à la somme des longueurs des 2 autres côtés. Le chemin, le plus cout, d'un point à un autre est la ligne droite. Un exercice donné en 5e va un peu plus loin. Son énoncé est le suivant :
Soit un triangle ABC tel que AB =6 et BC=9. Sachant que la mesure de AC est un nombe entier, quel est le plus grand périmètre possible pour le triangle ABC, quel est le plus petit périmètre possible. Justifier la réponse. Le fichier Géogébra permet de visualiser les questions et les réponses.
Il est possible de construire 4 familles de droite remarquables et leur intersection , un fichier visualise, ensemble, ou un par un :
- les médiatrices et propriétés de la médiatrice d'un
segment .
- les bissectrices des angles du triangle qui se coupent au même
point, le centre du cercle inscrit au triangle, il vous
est proposé, également un fichier
qui montre de façon ludique cette propriété.
- les hauteur qui se coupent au même point, l'orthocentre du triangle.
- les médianes qui se coupent au centre de gravité du triangle, situé au 2/3 de la longueur de la médiane, longueur comptée à partir du sommet. Le fichier Géogébra démontre cette propriété, pour comprendre cette démonstration il faut connaître le théorème de la droite des milieux ( triangle ) et le théorème de Thalès. Pour suivre la démo, utiliser la barre de navigation.
Le théorème de
Pythagore, grand classique du collège. L'énoncé du théorème de
pythagore , "dans
un triangle rectangle le carré de l'hypothénuse est égal à la somme des carrés des deux autres côtés"
génère chez les apprenants une série d'énoncés qui n'ont rien à voir
avec ce dernier. Plus long à dire, mais dit autrement: Dans
un triangle rectangle l'aire( surface) du carré ayant pour côté
l'hypothénuse, est égale à la somme des aires (surfaces)
des carrés ayant pour côté les deux autres côtés du triangle
rectangle. On devrait dire en effet : dans
un triangle rectangle le carré de la longueur
de l'ypothénuse est égal à la somme des carrés des longueurs
des deux autres côtés.La figure ci-contre montre bien
comment doit se comprendre ce théorème. Le carré
d'une longueur est une surface , il doit être égal à l'addition
d'autres surfaces. Parfois j'entends que le carré de l'hypothénuse est
égal au produit des deux autres côtés, ici on a bien surfce =surface ,
mais c'est faux, bien sûr. L'énoncé, le carré de l'hypothénuse est égal
à la somme des deux autres côtés, est incohérente puisque l'expression
d'une surface est déclarée ici égale à la somme de deux longueurs
m²=m!!. et j'entends souvent cette dernière proposition, on a bien
retenu carré et somme , ensuite on combine au hasard.
Toutes les démonstrations de ce
théorème font intervenir des longueurs " à la puissance
2, donc des surfaces géométriques.
Celle-ci reprend la figure ci
contre, deux "petits carrés" sont déformés, les figures
glissant et déformées vont occuper la totalité de la surface du
carré ayant pour côté l’hypoténuse. Pour suivre la suggestion de
démonstration, cochez la case, les carrés vont se colorer, et en
glissant le curseur les étapes de déformation, glissement vont
apparaître avec les commentaires.
Cette autre, plus
"synthétique " reprend la même démonstration , il suffit d’utiliser la
barre de défilement,en bas de la feuille, de l'étape 0 à 6. On la
retrouve sur le site Géogébra.
Une vidéo sur le net montre, entre autre, comment, avec une corde de de 13 noeux , et 12 segments de corde on peut construire un angle droit .
La réciproque du théorème de Pythagore
Le théorème de Pythagore suppose que
si un triangle est rectangle alors les 3 longueurs des côtés du triangle
rectangle sont reliées entre elles. Quand on connait 2 dimensions, on peut
calculer la troisième. et réciproquement si le carré de la longueur du plus grands des côtés est égal à la somme des longueurs des 2 autres côtés, le triangle est rectangle et le sommet de l'angle opposé au côté le plus grand est un angle droit.
Ci-contre la fenêtre du fichier Scratch qui illustre le théorème de Pythagore et sa réciproque, à droite triangle rectangle bleu, deux côtés sont connus, on peut calculer le troisième; à Gauche triangle orangé un point d'interrogation suggère qu'on ne sait pas si l'angle que l'on soupçonne d'être rectangle l'est vraiment, le script de Scratch déroule cette question. En lien ce script scratch téléchargeable et le fichier pdf qui l'explique. .
Pour aller plus loin il est utile d'observer ce qui se passe pour le ratio carré de la longueur de l’hypoténuse (ou de la plus grande longueur) / par la somme des longueurs des 2 autres côtés. Le fichie Scratch aborde cette question, elle est illustrée ici par un fichier Géogébra , observer comment évolue l'angle quand on déplace le sommet C au dela, sur ou à l'intérieur du cercle.
Une vidéo sur le net montre, entre autre, comment, avec une corde de de 13 noeux , et 12 segments de longueur égale, on peut construire un angle droit, en utilisant ici la réciproque du théorème de Thalès.
Théorème de Thalès, proportionnalité, Cosinus ...
Le schéma ci contre montre 3 copies écrans
du même fichier Géogébra qui
permet, en déplaçant le point rouge au centre ou les points A et D, de
faire apparaître différentes positions relatives des sécantes et
parallèles sans que l'égalité des rapports soit mise en cause.Un
autre fichier , extrait des ressources Géogébra donne sensiblement
les mêmes idées. Sinus, cosinus etc...
L'exploitation du théorème de Thalès, appliqué au triangle rectangle,
permet de comprendre les concepts de cosinus, sinus , tangente ...Le
fichier montre 3 triangles rectangles ayant un sommet commun, leur
base opposée à ce sommet sont parallèles, et toutes perpendiculaires
au côté de l'angle α commun. Un curseur permet de faire varier
l'angle α , le tableur affiche les donnés , longueur des côtés, le
calcul des quotients constants, comme celui, par exemple, du côté
opposé divisé par l’hypoténuse, quelque soit la position des trois
perpendiculaires. Il est possible de bouger ces perpendiculaires
en déplaçant les points bleus, en prime remarquer que
sinx²+cosx²=1 !
Quadrilatères
Du site Géogebra on y trouve des fichiers qui aident à comprendre :
- Tout d'abord la famille des quadrilatères du plus quelconque au plus "régulier", le carré.
- De façon plus détaillé ici
vous trouverez un fichier qui visualise le parallélogramme et sa
famille ( rectangle , losange, carré). En changeant l'angle entre les
deux diagonales( curseur a) on modifie la forme et les propriétés, on
peut modifier aussi le rapport de longueur des diagonales (curseur k ,
si k 1 , les diagonales sont égales), enfin il est possible de
modifier la taille de la figure ( curseur l). Le tout de façon
totalement indépendante. Enfin une case à cocher fait apparaître le
nom de la figure et les propriétés particulières qui lui sont
associées.
- ce fichier visualise
la somme des angles intérieurs et extérieurs d'un quadrilatère.
En déplaçant le curseur vous verrez comment la somme est suggérée.
- puis la terminologie à employer , pour désigner angles, côtés, etc.
- Enfin voici le nom de
certains polygones réguliers.
Cercle
Vocabulaire
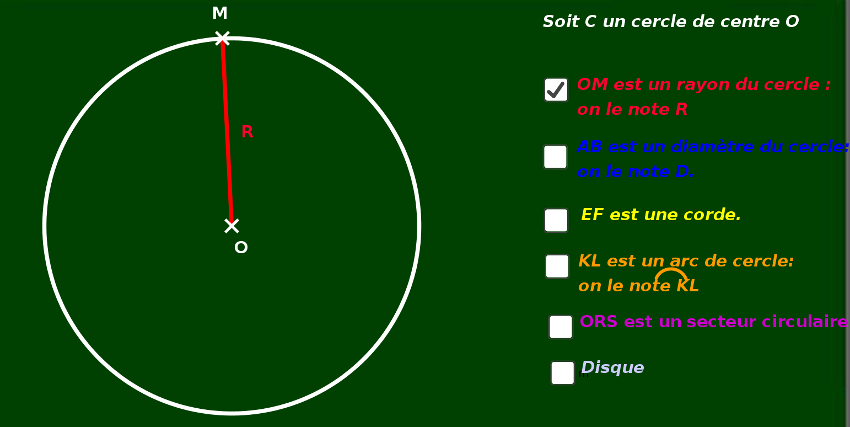Pour découvrir le
vocabulaire propre
aux divers éléments du cercle, aller ici. Vous ferez apparaître
chaque élément à l'aide des cases à cocher.
Périmètre du cercle.
Pour figurer le
rapport entre le diamètre du cercle et son périmètre ( sa
circonférence), c'est à dire le quotient de la division de la
circonférence par le diamètre du cercle , un fichier
montre un cercle, une roue, qui peut faire un tour complet ou partiel.
La distance parcourue en un tour complet correspond au périmètre du
cercle, on observera quand on fait varier le diamètre du cercle, comment
se comporte le rapport distance parcourue/diamètre. Que dire du
rapport Circonférence/ diamètre du cercle
Surface, aire du disque, appelé à tort, surface du cercle.
Deux fichiers proposent d'illustrer,
en deux temps, ce qu'est la surface du disque: Le
premier consiste en une animation qui permet de comprendre ce que
vaut la surface en fonction du rayon. Il suffit de lancer l'animation ,
le "cercle" de droite va se transformer en un triangle. Trois questions
(en anglais) apparaissent alors.
- En quoi la suface du cercle (disque) est comparable à celle du triangle?
- Utiliser seulement ce que vous avez observé pour proposer le calcul de la surface en utilisant les mots "circonférence" (du cercle) et "rayon".
- Montrer qu'il est possible d'écrire la formule en utilisant seulement le rayon!
La première réponse est "la surface du cercle origine est égale à la surface du triangle formé". Les 2 autres réponses se suffisent.
Attention pour les 2 fichiers cités ci-dessus, la figure doit être au départ constituée de 2 cercles , lancer alors l'animation que vous pouvez intérompre en cliquant sur PAUSE, pour recommencer ou démarrer correctement cliquez sur RESET.
Un autre fichier donne par une animation la compréhension de la valeur de cette surface par une animation astucieuse qu'il convient d'expliquer à l'apprenant.
les transformations
Symétries
- Symétrie centrale : Un fichier permet de découvrir la symétrie centrale, la construction, pas à pas, du symétrique d'un point par rapport à un centre, puis va plus loin jusqu'au symétrique d'un segment, il suffit de découvrir les étapes avec le curseur. Pour comprendre et expliquer : 5 figures dont on peut obtenir simplement les symétriques par rapport au centre symétrie, rouge sur la figure .
- symétrie axiale : Et voici un exercice simple qui consiste à déplacer des croix posées sur un point et à les placer au bon emplacement pour obtenir des points symétriques par rapport à un axe.
- Un exercice proposé en classe de cinquième permet de combiner symétrie centrale et axiale.
L'objectif: en partant de points placés
comme indiqué ci contre , créer un dessin constitué d'arcs de cercle ,
l'ensemble étant réalisé par des opérations de symétrie centrale ou axiale
, à partir de deux premiers arc de cercle exploitant les points
indiqués . 
Création des deux premiers demi-cercles et de leurs symétriques :
L'observation
des arcs montre qu'il s'agit de demi-cercles. L'outil Géogébra permet de
construire des demi-cercles, il suffit de connaître les extrémités qui
sont les extrémités du diamètre A' et A. A' est construit en créant le
symétrique de A dans la symétrie centrale de centre O, A' et A
sont sélectionnés dans cet ordre dans l'utilisation de l'outil Géogébra.
On crée de même B', symétrique de B dans la symétrie centrale de
centre I . Puis le demi cercle B'B est construit comme A'A. La première
figure qui sera reproduite 2 fois par symétrie axiale est terminée en
faisant "subir" aux deux demi-cercles une symétrie centrale de centre O,
Comme le montre l'image ci-dessous. le demi-cercle bleu pointillé est le
symétrique de B'B dans la symétrie centrale de centre O. Idem pour le
demi-cercle rouge pointillé par rapprt à B'1 . Il va falloir
répéter 2 fois cette figure , pour cela il faut construire les axes
auxiliaires de symétrie perpendiculaires à la droite AO . 
Poursuite de la construction
Une fois le premier axe de symétrie réalisé on peut procéder de 2 façons différentes :
- à l'aide l'outil symétrie axiale on répète l'opération : sélection de l'outil, sélection d'un des 4 demi-cercle, sélection de l'axe, le premier symétrique est tracé; on répète ainsi encore 3 fois la même opération pour tracer les 4 demi-cercles.
-
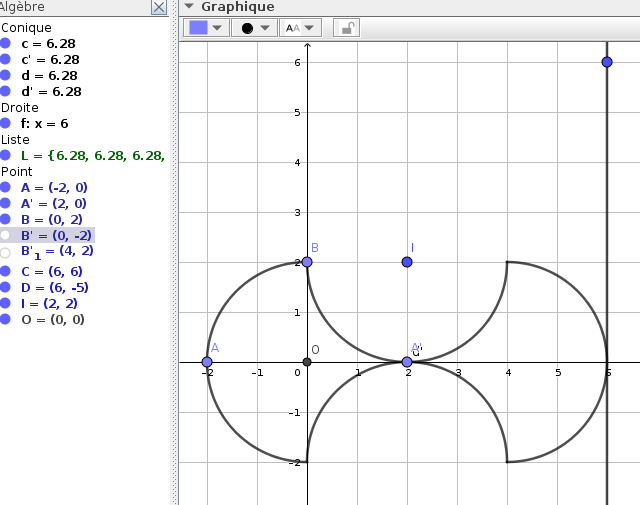plutôt que répéter 4 fois la même opération il est possible de
regrouper les 4 demi-cercles, sur la figureci-contre dans la fenêtre
algèbre les 4 demi-cercles sont rangés dans la catégories conique et
se nomment c, c', d, d'. Pour les regrouper il suffit de créer une
liste pour cela dans la zone de saisie on écrit :
La liste L est ainsi crée!
Pour créer le symétrique L' de L on peut procéder de 2 façons :
- soit cliquer sur l'outil symétrie axiale puis dans la zone fenêtre algèbre sélectionner successivement la ligne L puis la ligne droite f et L' se crée automatiquement
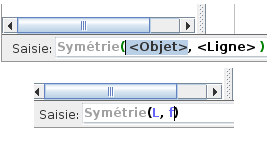soit
en ligne de saisie comme l'indique l'indique l'image ci-contre. L est
le nom la première liste, f est le nom de l'axe .
au final
Deux fichiers permettent d'observer le processus , il suffit pour cela d'utiliser la barre de navigation et de dérouler le processus. Le premier fichier n'exploite pas la notion de regroupement, de liste, le second exploite cette fonctionnalité.
Rotation.
Ce fichier permet de visualiser la différence de comportement d'une
symétrie centrale, axiale et une rotation, observer qu'une rotation de
360°, (demi-tour) se superpose à la symétrie centrale.
Translation
Ce fichier explique
comment résoudre ce problème : créer
un semis d'un dessin obtenu par rotation d' un triangle. une
succession de 5 rotations du triangle crée une étoile à 6 branches, une
succession de translations crée le semis. Le fichier final Géogébra est ici. Il
n’utilise que des outils simples, essentiellement graphiques, la fenêtre
algèbre s'étend beaucoup. Le dessin ci-contre est obtenu différemment en
faisant appel à des notions de Géogébra plus complexes que l'on n'
aborde peut-être pas en classe de quatrième , ce sont "liste" et
"séquence", quand on a assimilé ces outils , le résultat est plus
élégant, la fenêtre algèbre ne contient que quelques lignes, mais
est-il compréhensible au premier abord, je n'en suis pas sûr??.
Pour illustrer la translation , nous pouvons reprendre le sujet évoqué au paragraphe symétrie et résoudre la question par des symétries centrales pour la création de la figure de base , puis deux translations comme le montre le fichier et une vidéo qui montre le glissement des figures dans un sens et une longueur donnée.