Introduction
Il est frappant de constater que souvent les apprenants, quand ils parlent pour la première fois d'une pyramide , ils voient un triangle, pas un objet plus "complexe". Pour un prisme droit, ils parlent d'un rectangle ou un carré. Ils intègrent mal le passage des figures planes aux "volumes".
Il est très difficile de passer de l'étude des images planes cercle , triangle , etc figurées sur une feuille de papier ou un tableau , à l'étude de volumes que l'on présente, à plat, sur ces mêmes feuilles ou tableaux. Le lien entre la représentation sur une feuille et l'objet n'est pas évident. La représentation des volumes en perspective cavalière ( voir ci-dessous un extrait de l'article wikipedia sur le sujet)ou la confection des patrons posent problèmes. Les volumes 3D en bois ou en plastic aident, mais il faudrait, souvent, scier le cube ou la sphère par exemple pour que l'apprenant comprenne ce qu'est cette section, rectangle, cercle.... . Dans cette page , des fichiers Géogébra "3D" ont été sélectionnés et sont présentés, expliqués, ils doivent aider à comprendre ce sujet difficile. "La perspective cavalière est un outil qui permet de représenter sur une feuille de papier (en deux dimensions) des objets qui existent en volume (trois dimensions). Cette représentation ne présente pas de point de fuite : la taille des objets ne diminue pas lorsqu'ils s'éloignent."
Nota :
Géogébra 5 a présenté un dysfonctionnement pendant une longue période : la fenêtre 3D ne fonctionnait pas, aussi dans cette page , le lien pointe en premier lieu sur une page web , non pas sur un fichier *.ggb, le fichier *.ggb est proposé à la suite, pour ouverture si géogebra 5 ( ou 6) fonctionne ou pour être téléchargé.
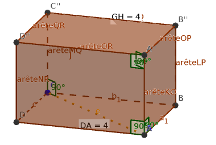
Parallélépipède
Pour représenter un parallélépipède rectangle,
encore appelé pavé droit, on trouve dans le site Geogebra la visualisation d'un pavé droit , et des cases à
cocher permettent de visualiser des sections , des coupures de ce
volumes de différentes manière, le fichier Geogebra* ,ggb est ici.

Cependant , l'apprenant a du mal à intégrer le dessin d'un volume sur
une feuille. Quand on lui montre un volume en bois , il ne parvient pas
toujours à imaginer, ce que donnerait un pavé coupé en 2.
Le document cité ci-dessus ne suffisant pas toujours, nous avons imaginé la section du pavé, par un plan parallèle à une arête et passant par une diagonale. Dans cette page, quand le curseur k est égal à zéro (k=0) le pavé droit est "entier". Quand k > 0 les deux prismes droits, ainsi formés, sont plus ou moins éloignés. Une face rectangulaire représentant la section est visible. Manipuler la figure 3D pour observer. On peut faire varier les 3 dimensions du pavé. Imaginons que le volume est une boite, de dimension l=3, L 4 , H =5 , peut-on y loger un spaghetti de 5 de long ? un bon moyen pour réviser Pythagore ! le fichier *.ggb est ici
Cette dernière page permet de visualiser la section
d'un parallélépipède rectangle par un plan quelconque défini par 3
points déplaçables chacun sur une arête définie, le fichier géogebra est
ici.
Pyramide
une première page permet de visualiser une pyramide quelconque, on peut modifier la forme de la base, le nombre de côtés, individuellement la dimension de ceux-ci, mais aussi position du sommet. Spontanément en choisissant le nombre de côtés, la figure formée sera de base régulière et le sommet sera placé sur la perpendiculaire de la base passant par le "centre" du cercle circonscrit au polygone régulier que constitue la base. A partir de cela on peut déplacer des sommets du polygone et en faire un polygone irrégulier et déplacer le sommet dans l'espace. L'axe de vision est réglable, on peut fermer et ouvrir la pyramide et faire ainsi apparaître le patron de celle ci.le fichier correspondant est ici .
Ce deuxième fichier permet de montrer des pyramides à base régulière

- ayant un nombre variable de côté de n= 3 à n=8,
- la hauteur est modifiable avec le curseur h
- quand les curseurs "décentrage" sont complètement à gauche le pied de la hauteur est confondu avec le cercle circonscrit au polygone régulier qui est la base, nous avons alors une pyramide régulière.
- On peut fermer et ouvrir le patron et observer ce que deviennent les faces latérales quand la pyramide est régulière.
- sur la figure ci contre le patron est ouvert , la base est un triangle équilatéral, les 3 faces des triangles isocèles
Cylindre
 Pour comprendre ce
que Signifie Cylindre de révolution
on peut se reporter ici
, j' ai extrait de cette page les images ci-jointes et le texte en
italique ci-dessous :
Pour comprendre ce
que Signifie Cylindre de révolution
on peut se reporter ici
, j' ai extrait de cette page les images ci-jointes et le texte en
italique ci-dessous :
Le mot révolution vient du latin volvere qui signifie « rouler ». Une expérience permet de mieux comprendre l'expression.
- On fixe un rectangle découpé dans du carton sur une perceuse de
façon que l'axe de la perceuse soit un axe de symétrie de la plaque.

- Quand on met en marche la perceuse, on a l'impression de voir un cylindre. Ce cylindre est engendré par les révolutions du rectangle autour de l'axe de symétrie, d'où le nom de cylindre de révolution.
A propos de l'expression de révolution. Les fichiers qui suivent vont essayer de figurer pour le cylindre puis le cône et enfin la sphère cette notion, à l'aide de fichiers Géogébra.
Tous les objets "tournés", vase de potier, pièce de bois telle que bobine de fil, bouton de bois, pied de lampe etc sont des objets "de révolution".
Des vidéos disponibles sur youtube montrent
comment sont réalisé des objets tournés, "de révolution" à partir de
morceau de bois plus ou moins diformes, voici deux liens :création d'un
saladier à partir d'un morceau de tronc d'arbre,
création de pièces d'art à partir d'une racine de buis. Dans
cette page , vous pouvez voir se former un cylindre ( de
révolution) , un cône ( de révolution) , une sphére à partir,
respectivement d'un rectangle, d'un triangle ou d'un demi cercle
tournant autour d'un axe bien choisi. Attention quand l'image devient
trop floue, vous ne pouvez effacer , fermer et relancer à partir du
navigateur, le fichier géogébra est ici
.
Cône
Intéressons nous au cône
de révolution. pour le décrire et le comprendre, nous verrons,
plus loin, le cône quelconque,
trois fichiers sont proposés pour celà.
 Tout d'abord découvrez comment se "forme " un cône de révolution,
c'est l’hypoténuse du triangle rectangle qui décrit le cône
quand le triangle rectangle tourne autour d'un côté de l'angle
droit. Voyez tourner cette hypoténuse et faites varier hauteur (h) et
rayon (r) de la base qui est un cercle. le fichier correspondant est ici.
Tout d'abord découvrez comment se "forme " un cône de révolution,
c'est l’hypoténuse du triangle rectangle qui décrit le cône
quand le triangle rectangle tourne autour d'un côté de l'angle
droit. Voyez tourner cette hypoténuse et faites varier hauteur (h) et
rayon (r) de la base qui est un cercle. le fichier correspondant est ici.
Cette troisième page permet de découvrir , le vocabulaire du cône de révolution , son patron et les grandeurs correspondantes, le fichier est ici .
Ce fichier permet d'observer la différence entre le cône de révolution et le cône quelconque. Dans ce fichier la base reste un cercle dont le centre est l'origine 0 des axes, il est possible de faire varier le rayon de 0.1 à 5, le sommet peut bouger, en faisant varier sa position dans un plan parallèle au plan du cône, en modifiant a et b, deux des coordonnées du sommet, le sommet est toujours à la même distance, c du plan de la base, sa hauteur reste constante tant que c ne varie pas. Après avoir modifier a, b, c ou r dans Géogébra sélectionner "affichage" puis "rafraîchir" . Quand S est "dans l'axe du cercle", sur la perpendiculaire au cercle en son centre, c'est à dire que la hauteur passe par le centre du cercle, le cône de révolution apparaît, si S est hors de l'axe, le cône de révolution disparaît. Pour visualiser le cône quelconque, bouger α , la génératrice SB va "bouger" laissant une trace qui visualise ce volume, pour recommencer après avoir modifier a, b, c , r ou α dans Géogébra sélectionner à nouveau "affichage" puis "rafraîchir". Si la forme se modifie, on observe que le volume du cône reste constant lorsque la hauteur et la base ne changent pas.
V=(1/3) surface de la base * hauteur.Sphère
Issu du travail du Collège Jule Verne Déville-les-Rouen, dans cette page on observera La section d'une sphère par un plan produit un cercle de section et deux solides nommés calottes sphériques. On peut déterminer le rayon HP du cercle de section en fonction de la distance OH du plan de coupe au centre de la sphère en appliquant le théorème de Pythagore au triangle rectangle OPH., le fichier correspondant est ici .
Les volumes plus "complexes"
 On rencontre dans la vie ,
certes, des volumes comme ceux décrits plus haut mais plus
souvent les volumes rencontrés sont plus ou moins des
associations de ces derniers.
On rencontre dans la vie ,
certes, des volumes comme ceux décrits plus haut mais plus
souvent les volumes rencontrés sont plus ou moins des
associations de ces derniers.
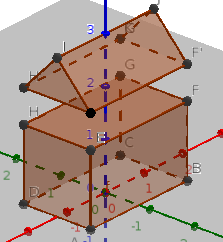
Imaginons un cylindre ou un prisme droit surmontés d'un cône ou d'une pyramide , à quoi pense t-on . cliquez ici et vous verrez se déplacer les"objets", quel est la surface des "objets" séparés et réunis? Dans le cas de la tour, combien y a-t-il d'arêtes et de faces sur les figures séparées? Combien, une fois celles-ci rassemblées?? le fichier correspondant est ici .
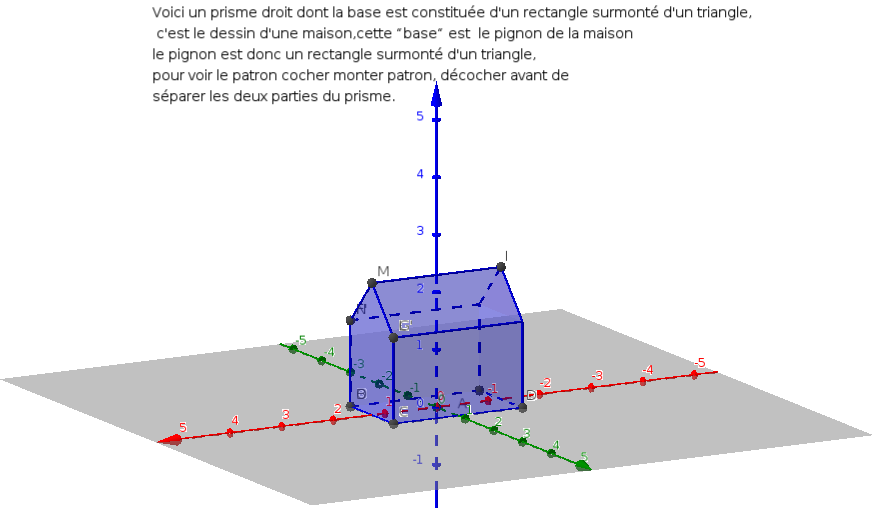 Observer
une maison simplifiée, essayer, en la regardant de plusieurs
façons, de la décomposer en 2 volumes un prisme droit à base
rectangulaire et un autre prisme droit à base triangulaire.
Combien y a-t-il d'arêtes et de faces sur les figures séparées ,
combien, une fois celles-ci rassemblées? Vous pouvez modifier, avec les
curseurs, l'aspect, regarder sur plusieurs angles, séparer les deux
parties. Les curseurs a et b représentent la longueur et la largeur de
la maison, Pour visualiser le patron , curseur de séparation
complètement à gauche, l'ensemble est bleu, cocher le patron, déplier
le. Pour voir l'éclaté décocher "monter patron", séparer les deux
parties et regarder dans l'orientation que vous souhaitez. Le fichier
*.ggb est ici .
Observer
une maison simplifiée, essayer, en la regardant de plusieurs
façons, de la décomposer en 2 volumes un prisme droit à base
rectangulaire et un autre prisme droit à base triangulaire.
Combien y a-t-il d'arêtes et de faces sur les figures séparées ,
combien, une fois celles-ci rassemblées? Vous pouvez modifier, avec les
curseurs, l'aspect, regarder sur plusieurs angles, séparer les deux
parties. Les curseurs a et b représentent la longueur et la largeur de
la maison, Pour visualiser le patron , curseur de séparation
complètement à gauche, l'ensemble est bleu, cocher le patron, déplier
le. Pour voir l'éclaté décocher "monter patron", séparer les deux
parties et regarder dans l'orientation que vous souhaitez. Le fichier
*.ggb est ici .